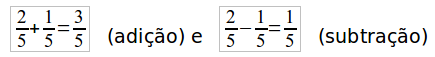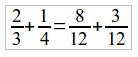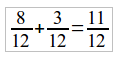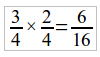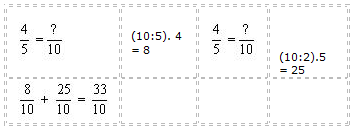PORCENTAGEM
É frequente o uso de expressões que refletem acréscimos ou reduções em preços, números ou quantidades, sempre tomando por base 100 unidades. Alguns exemplos:
- A gasolina teve um aumento de 15%
Significa que em cada R$100 houve um acréscimo de R$15,00
- O cliente recebeu um desconto de 10% em todas as mercadorias.
Significa que em cada R$100 foi dado um desconto de R$10,00
- Dos jogadores que jogam no Grêmio, 90% são craques.
Significa que em cada 100 jogadores que jogam no Grêmio, 90 são craques.
Razão centesimal
Toda a razão que tem para consequente o número 100 denomina-se razão centesimal. Alguns exemplos:
Podemos representar uma razão centesimal de outras formas:
As expressões 7%, 16% e 125% são chamadas taxas centesimais ou taxas percentuais.
Considere o seguinte problema:
João vendeu 50% dos seus 50 cavalos. Quantos cavalos ele vendeu? Para solucionar esse problema devemos aplicar a taxa percentual (50%) sobre o total de cavalos.
Logo, ele vendeu 25 cavalos, que representa a porcentagem procurada.
Portanto, chegamos a seguinte definição:
Porcentagem é o valor obtido ao aplicarmos uma taxa percentual a um determinado valor.
|
Exemplos:
Calcular 10% de 300. 
Calcular 25% de 200kg.

Logo, 50kg é o valor correspondente à porcentagem procurada.
EXERCÍCIOS:
1) Um jogador de futebol, ao longo de um campeonato, cobrou 75 faltas, transformando em gols 8% dessas faltas. Quantos gols de falta esse jogador fez?
Portanto o jogador fez 6 gols de falta.
2) Se eu comprei uma ação de um clube por R$250,00 e a revendi por R$300,00, qual a taxa percentual de lucro obtida?
Montamos uma equação, onde somando os R$250,00 iniciais com a porcentagem que aumentou em relação a esses R$250,00, resulte nos R$300,00.
Portanto, a taxa percentual de lucro foi de 20%.
Uma dica importante: o FATOR DE MULTIPLICAÇÃO.
Se, por exemplo, há um acréscimo de 10% a um determinado valor, podemos calcular o novo valor apenas multiplicando esse valor por 1,10, que é o fator de multiplicação. Se o acréscimo for de 20%, multiplicamos por 1,20, e assim por diante. Veja a tabela abaixo:
| Acréscimo ou Lucro | Fator de Multiplicação |
| 10% | 1,10 |
| 15% | 1,15 |
| 20% | 1,20 |
| 47% | 1,47 |
| 67% | 1,67 |
Exemplo: Aumentando 10% no valor de R$10,00 temos: 10 * 1,10 = R$ 11,00
No caso de haver um decréscimo, o fator de multiplicação será:
Fator de Multiplicação = 1 - taxa de desconto (na forma decimal)
Veja a tabela abaixo:
| Desconto | Fator de Multiplicação |
| 10% | 0,90 |
| 25% | 0,75 |
| 34% | 0,66 |
| 60% | 0,40 |
| 90% | 0,10 |
Exemplo: Descontando 10% no valor de R$10,00 temos: 10 * 0,90 = R$ 9,00